
问题描述
一共有三个柱子,其中一个柱子上放着若干大小都不等的圆盘,最大的圆盘在最下面,而最小的圆盘在最上面。通过一些移动,使得所有的原盘都移动到另一个柱子上,依旧保持上小下大。而移动的规则是:每次只能移动一个圆盘,且小盘永远不能处于大盘上方。为了达到这个目的,最少需要多少次移动?
解决和证明
引入几个概念
- 初始柱子:最开始时,所有圆盘所处的柱子
- 目标柱子:最终完成时,所有圆盘所处的柱子
- 中间柱子:除了初始柱子和目标柱子以外的柱子
给出一种递归解
假设一共有 $n$ 个圆盘。首先,我们把初始柱子最上面的 $n-1$ 个圆盘移动到中间柱子上。之后,把初始柱子上最大的圆盘移动到目标柱子上。最后,把中间柱子上的 $n-1$ 个圆盘移动到目标柱子上,这样就能完成移动了。那么, $n-1$ 个圆盘应该如何移动呢?其实,把 $n-1$ 个圆盘移动到中间柱子上的问题,是等价于具有 $n-1$ 个圆盘的汉诺塔问题的。通过递归,问题最后会转变成只有1个圆盘的汉诺塔问题,1个圆盘怎么移动用屁股想都知道了。我们使用 $T_n$ 来表示该方法在具有 $n$ 个圆盘时的移动次数,那么我们就可以得到:
$$ T_n\leq2T_{n-1}+1 $$证明递归解最优
上面给出了一种可行的移动方法,那么这个解法是不是最优解呢。没错,这就是最优解,下面来说明这一点。为了完成汉诺塔的移动,初始柱子上的最大盘必然会经历第一次从初始柱子上移走的情况,同时,必然有一个柱子是空的来接受最大盘,因为没有任何一个盘子能处在最大盘的下方,所以,其他所有的盘子都必然是有序地处在一个柱子上,把这次移动完成之前的状态记为状态A。同样的道理,目标柱子上必然会经历最大盘最后一次移动到该柱子上,而其他两个柱子的情况也是一个为空、一个为满,把这次移动完成之后的状态记为状态B。从初始状态变为状态A最少需要移动的次数为 $T_{n-1}$ ,从状态B变为结束状态最少需要移动的次数也为 $T_{n-1}$ ,而从状态A变为状态B至少需要1次移动(不可能是0次)。所以我们就可以得到:
$$ T_n\geq2T_{n-1}+1 $$结合由可行解得到的不等式,我们就可以确定一组递归式:
$$ T_n=\begin{cases}0&n=0\\ 2T_{n-1}+1&n>0\\ \end{cases} $$解递归式就可以得到该解法的封闭形式答案: $T_n=n^2-1$ 。(可以通过递归式两边各加1,然后换元求解)
变种问题
- 有 $2n$ 个盘子,共有 $n$ 种大小的尺寸,每种尺寸都为两个,而且同样大小的盘子不区分。这种情况最少需要移动多少次?
- 条件同上,但是同样大小的盘子需要区分,移动到目标柱子上后需要保持和原先一样的上下顺序。这种情况最少需要移动多少次?
- 初始柱子和目标柱子之间不再能够直接移动,必须先移动到中间柱子中转。这种情况下最少需要移动多少次?
任意状态转移
如果汉诺塔的初始状态不再是所有圆盘都处在初始柱子上,而是任意一种情况。同时,结束状态也是任意一种情况。那么这样的情况下,是不是能够在 $2^n-1$ 次内完成移动呢?没错,是这样的。我们给出这样一种递归的解法,如果初始状态和结束状态的最大盘是处于同一柱子上的,这就表明他们是不需要移动的。问题就转换成 $n-1$ 的情况。如果是不在同一个柱子上的情况,我们移动所有除了最大盘的盘子到中间柱子,然后移动最大盘到目标柱子,这样问题就转换成 $n-1$ 的情况了。通过这种递归操作,问题就解决了。假设移动的次数为 $M_n$ ,最后我们可以得到: $M_n\leq2^n-1$ 。
如果我们把所有的状态都表示成一个节点,一次移动表示成一条边,就可以画出一个状态转移图。从图中我们就可以很直观地看出许多规律了。a、b、c分别代表三个柱子,abc表示:最小盘在a柱、中等盘在b柱、最大盘在c柱。
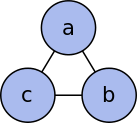
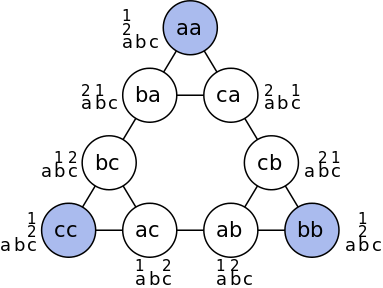
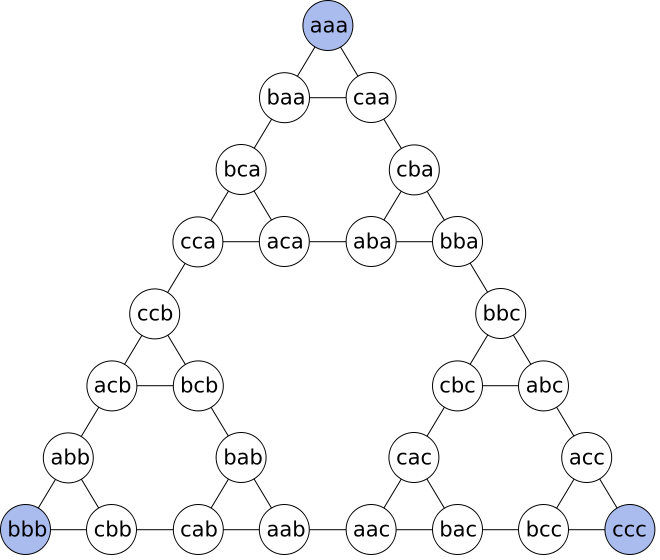
四个柱子的情况
现在我们升级一下汉诺塔问题,柱子从三个变成了四个,一个初始柱子、两个中间柱子、一个目标柱子。最少需要多少次移动?
给出一种递归解
移动初始柱子最上方的 $k$ 个盘子到中间柱子,再把初始柱子上剩余的 $n-k$ 个盘子移动到目标柱子上,最后再把中间柱子上的 $k$ 个盘子移动到目标柱子上。假设四个柱子的汉诺塔问题的最优解为 $M_n$ ,三个柱子的最优解依旧为 $T_n$ 。那么我们就可以得到:
$$ M_n\leq2M_k+T_{n-k} $$那么这个解法是不是最优解呢?也就是说等式能否成立,答案是肯定的。四个柱子的证明直到2014年才被完成,所以我也不知道怎么证明。证明的论文在 这里,似乎是法语写的。 $k$ 值的取值有下面这个公式给出(round表示四舍五入):
$$ k=n-round\left(\sqrt{2n+1}\right)+1 $$通用的问题描述
泛化汉诺塔问题,假设有 $n$ 个盘子, $r$ 个柱子,最优解为 $T\left(n,r\right)$ 。
Frame-Stewart算法
上面说到的递归解就是Frame-Stewart算法的特殊形式,也就是 $r=4$ 情况。这个算法都是先移动最上方的 $k$ 个圆盘,再移动剩下的,再移动 $k$ 个圆盘到目标柱子。那么递归解就会是:
$$T\left(n,r\right)=2T\left(k,r\right)+T\left(n-k,r-1\right) $$$k$ 的取值公式同上。对于 $r>4$ 的情况都是还未得到证明的。
一种笨办法
我们可以把状态转移图输入给计算机,通过计算图的最短路径来获得任意两个状态之间的最少移动次数。但是这种方法会消耗大量的时间,且只能用在图规模不大的情况下。